Type Equality in LLVM
Published on
Some months ago, I joined ShiftLeft Security to work on the LLVM support for the custom code analysis platform Ocular. During these months, we have faced and overcome several challenges.
Here I want to share one of them: Type Equality in LLVM.
Intro
LLVM’s type system is a complicated topic. It attempts to solve problems that are not so obvious when you look at them from a high-level. Recently, I had a chance to dive deeper into the subject and discovered that while the current implementation makes some things more straightforward, some other parts are counter-intuitive and may not meet your expectations.
In this article, I want to describe some limitations of the LLVM type system and share how we solved one particular problem: detecting equivalent types in LLVM. The article is organized as follows: I start with the recap of the LLVM type system, followed by the problem statement, then describe how we attempted to solve the issue using existing LLVM features, and finally conclude with the solution we came up with.
LLVM Type System recap
It is highly recommended to read this post from Chris Lattner explaining some of the considerations that were taken into account when the type system was revised around LLVM 3.0: LLVM 3.0 Type System Rewrite.
Just a few random words on the current type system (if you didn’t read the linked article):
- types belong to an
LLVMContext - instances of each type allocated on the heap (e.g.,
llvm::Type *type = new llvm::Type;) - type comparison is done via pointer comparison
- types in LLVM go into three groups: primitive types (integers, floats, etc.), derived types (structs, arrays, pointers, etc.), forward-declared types (opaque structs)
Problem Statement
Consider the following example:
// Point.h
struct Point {
int x;
int y;
};
// foo.c
#include "Point.h"
// use struct Point
// bar.c
#include "Point.h"
// use struct Point
When foo.c and bar.c compiled down to the LLVM IR (foo.ll and bar.ll) they both
have the struct Point defined as follows:
%struct.Point = type { i32, i32 }
Though, when both IR files loaded in one context, the type names changed to prevent name collisions, so they end up being defined as
%struct.Point = type { i32, i32 }
%struct.Point.0 = type { i32, i32 }
We want to deduplicate such types.
Our (failed) attempts
We made several attempts to solve the problem using simple heuristics and built-in LLVM features.
It went wrong in many ways.
‘Types with the same name are the same type’ (false)
This is a very simple heuristic:
%struct.Point = type { i32, i32 }
%struct.Point.0 = type { i32, i32 }
If we strip the numeric suffix that is added by LLVM, then the types have the same name, and therefore they are the same. This is a good idea, but it does not work. This is a perfectly valid LLVM bitcode:
%struct.Point = type { i32, i32 }
%struct.Point.0 = type { float, float, float }
for which our heuristic does not apply.
Primitive Types Equality
In LLVM, types belong to the LLVMContext. Primitive types such as int32, float, or double pre-allocated
and then reused. In the context of LLVMContext (pun intended), you can only create one instance of a primitive type.
With this solution, it is easy to check if types are the same - simply compare the pointers.
However, this solution cannot work if you want to compare types from different contexts.
According to LLVM, int32 from one LLVMContext differs from int32 from another LLVMContext,
even though they are the same type according to intuition.
Struct Types Equality
This situation gets even more complicated when it comes to identified (named) structs.
Consider the same example I gave initially.
// Point.h
struct Point {
int x;
int y;
};
// foo.c
#include "Point.h"
// use struct Point
// bar.c
#include "Point.h"
// use struct Point
So far so good, but as mentioned previously, LLVM keeps both types and renames one of them to prevent name collisions:
%struct.Point = type { i32, i32 }
%struct.Point.0 = type { i32, i32 }
Even though these are the same types from a user perspective, they are very different from the LLVM’s point of view. Therefore, we cannot use pointer comparison: the types are distinct and point to different memory regions. In this case, the best we can do is to compare the layout of the types and consider them equal if the layouts are identical.
The good part is that LLVM has a function for that: llvm::StructType::isLayoutIdentical.
The bad part is that this function is broken. Consider the following example:
%struct.Point = type { i32, i32 }
%struct.Point.0 = type { i32, i32 }
%struct.wrapper = type { %struct.Point }
%struct.wrapper.0 = type { %struct.Point.0 }
According to LLVM, the layouts of struct.Point and struct.Point.0 are identical, while the layouts of struct.wrapper and
struct.wrapper.0 are not: isLayoutIdentical returns true only when all the type elements of the struct are equal.
And this equality is checked via pointer comparison.
IRLinker/llvm-link
LLVM has a class that merges two modules into one: IRLinker. LLVM also comes with a CLI tool llvm-link, which does the same.
The IRLinker works fine, but far away from being good: it drops important information.
The following IR after running through IRLinker
%struct.Point = type { i32, i32 }
%struct.Tuple = type { i32, i32 }
becomes
%struct.Point = type { i32, i32 }
dropping the other struct since both have the same layout. We don’t want to lose this information.
Moreover, IRLinker does another kind of magic that may introduce types that never existed at the source code level.
This is what I’ve seen after running llvm-link on the XNU kernel bitcode:
%struct.tree_desc_s = type {
%struct.ct_data_s*,
i32,
%struct.mach_msg_body_t*
}
%struct.tree_desc_s.79312 = type {
%struct.ct_data_s*,
i32,
%struct.static_tree_desc_s*
}
Notice the different types of the third element: struct.mach_msg_body_t* vs struct.static_tree_desc_s, even though there is only one definition of tree_desc_s at the source code level:
struct tree_desc_s {
ct_data *dyn_tree;
int max_code;
static_tree_desc *stat_desc;
};
So the IRLinker did something odd, at which point I gave up all the attempts to understand how it works and what it does.
Our solution to this problem
I could not find any other solution to the problem, so we decided to roll out our own.
A bit of background
Our implementation is inspired by Tree Automata and Ranked Alphabets.
Here is a short description: a ranked alphabet consists of a finite set of symbols F, and a function Arity(f), where f belongs to the set F.
The Arity tells how many arguments a symbol f has. Symbols can be constant, unary, binary, ternary, or n-ary.
Here is an example of the notation: a, b, f(,), g(), h(,,,,). a and b are constants, f(,) is binary, g() is unary, and h(,,,,) is n-ary.
The arity of each symbol is 0, 0, 2, 1, and 5, respectively.
Given the alphabet a, b, f(,), g() we can construct a number of trees:
- f(a, b)
- g(b)
- g(f(b, b))
- f(g(a), f(f(a, a), b))
- f(g(a), g(f(a, a)))
etc.
If we know the arity of each symbol, then we can omit parentheses and commas and write the tree as a string. The tree is constructed in the depth-first order, here are the same examples as above, but in the string notation:
- fab
- gb
- gfbb
- fgaffaab
- fgagfaa
Here is a more comprehensive example:
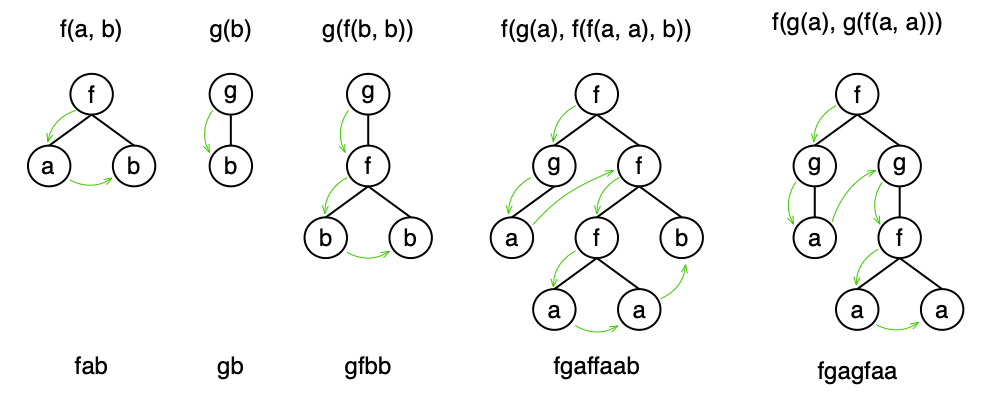
The arrows show the depth-first order.
We can map our type equivalence problem on the ranked alphabet/tree automaton concepts.
Type Equality
We consider each type to be a symbol, and its arity is the number of properties we want to compare. Then, we build a tree of the type and convert it to the string representation. If two types have the same string representation, then they are equal.
Some examples:
i32,i64,i156: symbolI, arity is 1 since we only care about bitwidth (e.g., 32, 64, 156)float: symbolF, arity is 0, allfloattypes are the same[16 x i32]: symbolA, arity is 2, we care only about the length of the array and its element typei8*: symbolP, arity is 1, we care only about the pointee type{ i32, [16 x i8], i8* }: symbolS, arity is number of elements + 2. We want to store the struct ID and number of its elements.
If we care about more or fewer values, then we can simply change the arity for a given symbol. Examples of types represented as a tree:
i32->I(32)->I32i177->I(177)->I177[16 x i8*]->A(16, P(I(8)))->A16PI8{ i32, i8*, float }->S(3, S0, I(32), P(I(8)), F)->S3S0I32PI8F
Note: the values in S are the number of elements (3), struct ID (S0), and all its contained types defined recursively.
Same types, but represented graphically:
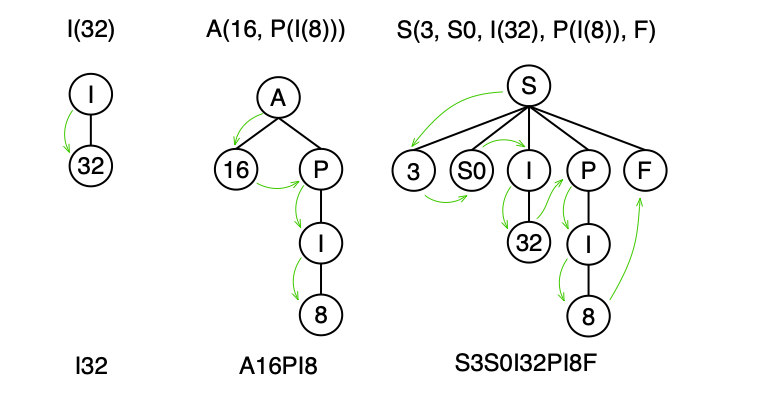
Structural Equality
Above, I mentioned the struct ID. We need it to define the structural equality for recursive types.
Consider the following example:
%list = type { %list*, i32 }
%node = type { %node*, i32 }
%root = type { %node*, i32 }
All of the above structs have the same layout: a pointer + an integer. But we do not consider them all to be equal. By our definition of equality the following holds:
list == node
root != node
root != list
The reasoning is simple: the list and node has the same layout and the same structure (recursive), while root has another structure.
Here is a graphical representation to highlight the idea. If we discard the struct titles, then it’s clear the first two are equal while the third one is distinct.
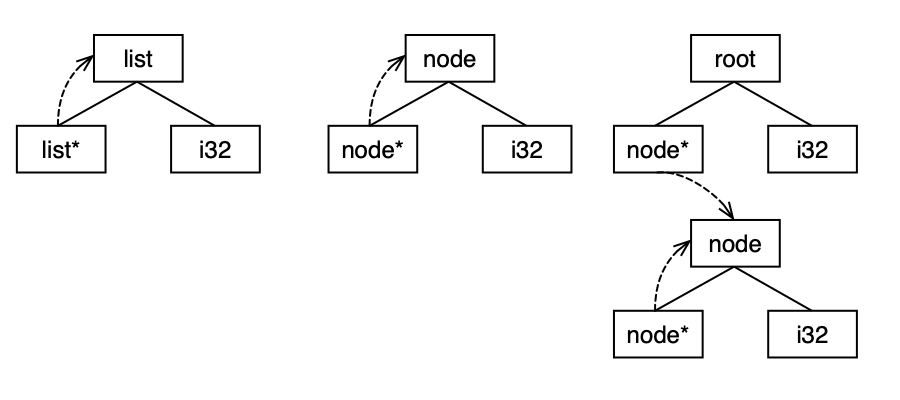
To take the structure into account and to make the equality hold, we do not use the names of the structures, but before building the tree, we assign them symbolic names or IDs.
So both the list and node encoded as the following: S(2, S0, P(S(2, S0, x, x), I(32)) where S0 is the struct ID. To terminate the recursion we do not re-emit types for the structure that has already been emitted, but we do emit symbols x instead (otherwise we won’t respect the arity of the struct).
The root is defined as follows S(2, S0, P(S(2, S1, P(S(2, S1, x, x), I(32), I(32))), I(32)) please note the nestedness and S0 and S1 struct IDs.
Given these two encodings, the comparison above holds.
Opaque Struct Equality
Comparing opaque structs is as easy as the comparison of infinities. It’s totally up to us how we define this property.
The right and sound approach is to say that the opaque struct equals only to itself, but we need to do better than this.
For opaque structs, we also use symbolic names. But different opaque structs get the same symbolic name as soon as they have the same canonical name.
Example:
%struct.A = type opaque
%struct.A.0 = type opaque
%struct.B = type opaque
%foo = type { %struct.A* }
%bar = type { %struct.A.0* }
%buzz = type { %struct.B* }
Here, the canonical names for the opaque structs are A (%struct.A, %struct.A.0) and B (%struct.B).
Therefore, we treat the %struct.A and %struct.A.0 as equal, while %struct.B is not equal to the either of As.
Even though all of the 3 structs can point to the same type or completely different types.
Letters, symbols, and IDs
While IMO, letters and symbols are easier to work with for a human being, I implemented all the encodings as vectors of numbers. It is then easy to get a hash of such vector and add some memoization for better performance, even though I didn’t spend any time measuring and looking for bottlenecks.
Conclusion
To conclude, I’d say that one should not rely on the built-in capabilities of LLVM to compare types. In fact, IRLinker uses a very different algorithm.
The algorithm I described has drawbacks, and I probably missed some edge cases. But anyway, I would love to get some feedback on it, and I hope it may help someone who gets into a similar situation.
